Transit Note #129

DPGA Utilization and Application

Andre DeHon

Original Issue: September, 1995

Last Updated: Fri May 17 20:10:30 EDT 1996

Abstract:

Introduction

FPGA capacity is conventionally metered in terms of ``gates'' assigned to a problem. This notion of gate utilization is, however, a purely spatial metric which ignores the temporal aspect of gate usage. That is, it says nothing about how often each gate is actually used. A gate may only perform useful work for a small fraction of the time it is employed. Taking the temporal usage of a gate into account, we recognize that each gate has a capacity defined by its bandwidth. Exploiting this temporal aspect of capacity is necessary to extract the most performance out of reconfigurable devices.

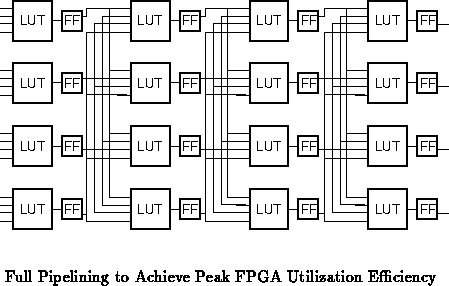
To first order, conventional FPGAs only fully exploit their potential gate capacity when fully pipelined to solve a single task with data processing rates that occupy the entire array at its maximum clock frequency. In the extreme, each pipeline stage contains a minimum amount of logic and interconnect (See Figure ). As task requirements move away from this extreme, gates are used at a fraction of their potential capacity and FPGA utilization efficiency drops.

Away from this heavily pipelined extreme, multiple context devices, such as DPGAs, provide higher efficiency by allowing limited interconnect and logic element resources to be reused in time. These devices allow the temporal component of device capacity to be deployed to increase total device functionality rather than simply increasing throughput for fixed functionality.

In this paper we examine several, stylized usage patterns for DPGAs focusing on the resource reuse they enable. We start by identifying capacity and utilization metrics for programmable devices (Section ). We examine a few characteristics of application and technology trends (Section ) to understand why resource reuse is important. In Section we briefly review DPGA characteristics and look at the costs for supporting resource reuse. The heart of the paper then focuses on four broad styles for resource reuse:

• Multiple, Independent Functions (Section )
• Utility Functions (Section )
• Temporal Pipelining (Section )
• Finite State Machines (Section )

Capacity and Utilization

An FPGA is composed of a number of programmable gates interconnected by wires and programmable switches. Each gate, switch, and wire has a limited bandwidth () --- or time between uses () necessary for correct operation. In a unit of time , we could, theoretically, get a maximum of gate evaluations, and switch and wire traversals.

Each gate, switch, and wire has an inherent propagation latency () as well.

For simplicity, let us model an FPGA as having a single, minimum reuse time, , which is the minimum reuse time for a gate evaluation and local interconnect. We will assume captures both the bandwidth and the propagation delay limitations. The flip-flop toggle rate which was often quoted by vendors as a measure of device performance [Xil94], provides a rough approximation of for commercial devices ( i.e. ). Throughout, we assume to allow simple time discretization and comparison.

The peak operational capacity of our FPGA is thus:

may be any of the potentially limited device resources such as gates, wires, or switches. This peak capacity is achieved when the FPGA is clocked at and every gate is utilized. In our conventional model, that means every gate registers its output, and there is at most one logic block between every pair of flip flops (See Figure ). This is true even when the register overhead time is not small compared to , but the computation latency may be increased noteably in such a case.

When we run at a slower clock rate to handle deeper logic paths, or the device goes unused for a period of time, we get less capacity out of our FPGA. Running at a clock rate , we realize a gate utilization:

As and , the utilization is below capacity. For example, if the path delay between registers is four gate-interconnect delays (See Figure ), such that , even if all the device gates are in use, the gate utilization, , is one-quarter the peak capacity . more_utilization.tex

Technology and Application Trends

Utilization of a resource is only important to the extent that one is capacity limited in that resource. For example, if an FPGA has a plethora of gates, but insufficient switching to use them, gate utilization is irrelevant while switch utilization is paramount. When one resource is limited, pacing the performance of the system, we say this resources is the bottleneck. To improve performance we deploy or redeploy our resources to utilize the bottleneck resource most efficiently. In this section we look at the effects of bottlenecks arising from application requirements and from technology-oriented resource costs.

Bottlenecks and Capacity

The first question to ask is: ``Why do we not fully pipeline every design and run it at the maximum clock frequency?'' The primary answer, aside from design complexity, is that we often do not need that much of every computation. While heavy pipelining gets the throughput up for the pipelined design, it does not give us any more functionality, which is often the limiter at the application level.

Relative Processing Speeds

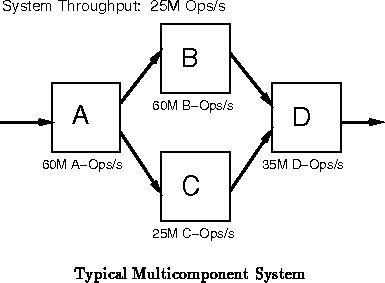
In these situations, reuse of the active silicon area on the non-bottleneck components can improve performance or lower costs. If we are getting sufficient performance out of the bottleneck resource, then one may be able to reduce cost by sharing the gates on the non-bottleneck resources between multiple ``components'' of the original design (See Figure ). If we are not getting sufficient performance on the bottleneck resource and its task is parallelizable, we may be able to employ underused resources on the non-bottleneck components to improve system performance without increasing system cost (See Figure ).

Fixed Functional Requirements

Technology and Bottleneck Resources

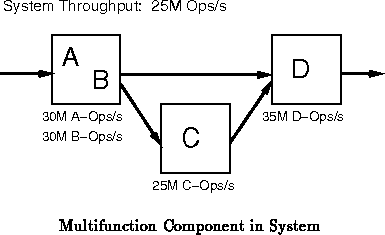
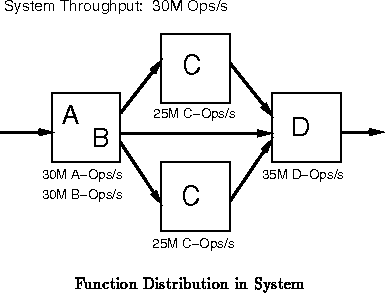
Many bottlenecks arise from implementation technology costs. Resources which are relatively ``expensive'' in area, have inherently high latencies, or have inherently low bandwidths tend to create bottlenecks in designs. I/O and wiring resources often pose the biggest, technology-dictated bandwidth limitations in reconfigurable systems.

I/O Latency and Bandwidth

When data throughput is limited by I/O bandwidth, we can reuse the internal resources to provide a larger, effective, internal gate capacity. This reuse decrease the total number of devices required in the system. It may also help lower the I/O bandwidth requirements by grouping larger sets of interacting functions on each IC.

Routing

Latency Limited Designs

Some designs are limited by latency not bandwidth. Here, high bandwidth may be completely irrelevant or, at least, irrelevant when it is higher than the reciprocal of the design latency. This is particularly true of applications which must be serialized for correctness ( e.g. atomic actions, database updates, resource allocation/deallocation, adaptive feedback control).

By reusing gates and wires, we can use device capacity to implement these latency limited operations with less resources than would be required without reuse. This will allow us to use smaller devices to implement a function or to place more functionality onto each device.

Cyclic dependencies

Some computations have cyclic dependencies such that they cannot continue until the result of the previous computation is known. For example, we cannot reuse a multiplier when performing exponentiation until the previous multiply result is known. Finite state machines (FSMs) also have the requirement that they cannot begin to calculate their behavior in the next state, until that state is known. In a purely spatial implementation, each gate or wire performs its function during one period and sits idle the rest of the cycle. Resource reuse is the most beneficial way to increase utilization in cases such as these.

DPGA Characteristics

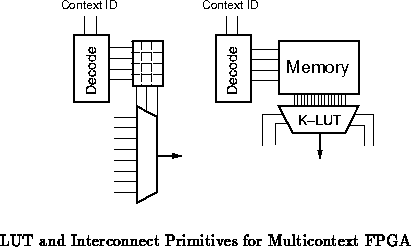
In multicontext FPGAs, we increase utilization, , by allocating space on chip to hold several configurations for each gate or switch. Rather than having a single configuration memory, each Look Up Table (LUT) or multiplexor, for instance, has a small local memory (See Figure ). A broadcast context identifier tells each primitive which configuration to select at any given point in time.

By allocating additional memory to hold multiple configurations, we are reducing the potential for a fixed amount of silicon. At the same time, we are facilitating reuse which can increase utilization. Multiple contexts are beneficial to the extent that the additional space for memory creates a net utilization increase.

Let us consider our array as composed of context memory occupying a fraction of the die and active area occupying . For simplicity, we assume . We can now relate the multicontext peak to the single-context FPGA peak:

We can calculate multicontext gate utilization, for example:

We can calculate an efficiency for the use of active multicontext resources:

Alternately, we can compare total silicon utilization efficiency to the single context case:

Equation computes the net utilization efficiency of the silicon. This is the quantity we need to maximize to get the most capacity out of our silicon resources.

Breaking up the area by number of contexts, :

In Equation , we use instead of since we assume base silicon usage () includes one configuration and any fixed overhead associated with it. is the incremental cost of one context configuration's worth of memory. To the extent the size of the context configuration is linear in the size of the device, we can approximate as proportional to :

This gives us:

or

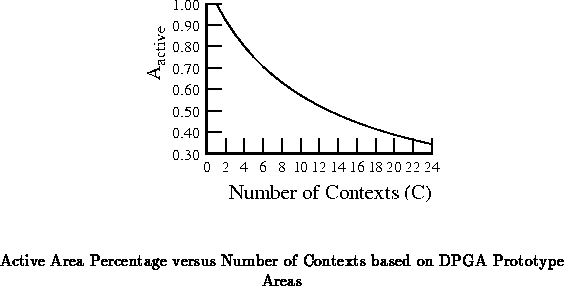
Our first generation DPGA prototype [TEC +95a] was implemented in a 3-layer metal, 1.0m CMOS process. The prototype used 4-LUTs for the basic logic blocks and supported 4 on-chip context memories. Each context fully specified both the interconnect and LUT functions. Roughly 40% of the die area consumed on the prototype went into memory. We estimate that half of that area is required for the first context, while the remaining area is consumed by the additional three contexts. For the prototype implementation, then, 20% and 80%. Based on the relative sizes in the prototypes and using the above relations, this gives (, , , ). With these technology constants, Equation becomes:

Figure plots the relationship shown in Equation .

Context switch overhead associated with reading new configuration data can further decrease multicontext capacity by increasing over . Our experience suggests that unpipelined context changes yield a . This effect can be minimized by pipelining the context read at the cost of the additional area for a bank of context registers (lowering ). We make the pedagogical assumption that for this discourse.

Multiple Independent Functions

The easiest and most mundane way to increase the utilization on an FPGA is to use the FPGA for multiple, independent functions. At a very coarse granularity, conventional FPGAs exploit this kind of reuse. The essence of reconfigurable resources is that they do not have to be dedicated to a single function throughout their lifetime. Unfortunately, with multi-millisecond reconfiguration time scales, this kind of reconfiguration is only useful in pushing up utilization in the coarsest or most extreme sense. Since conventional devices do not support background configuration loads, the active device resources are idle and unused during these long reconfiguration events. Reload time thus contributes to (Equation ).

With multiple, on-chip contexts, a device may be loaded with several different functions, any of which is immediately accessible with minimal overhead. A DPGA can thus act as a ``multifunction peripheral,'' performing distinct tasks without idling for long reconfiguration intervals. In a system such as the one shown in Figure , a single device may perform several tasks. When used as a reconfigurable accelerator for a processor ( e.g. [AS93] [DeH94a] [RS94]) or to implement a dynamic processor ( e.g. [WH95]), the DPGA can support multiple loaded acceleration functions simultaneously. The DPGA provides greater capacity by allowing rapid reuse of resources without paying the large idle-time overheads associated with reconfiguration from off-chip memory.

In a data storage or transmission application, for instance, one may be limited by the network or disk bandwidth. A single device may be loaded with functions to perform:

• (De)compression
• Cryptographic ( e.g. DES) (de)encoding
• ECC Calculation, error detection, and correction

Within a CAD application, such as espresso [RSV87], one needs to perform several distinct operations at different times, each of which could be accelerated with reconfigurable logic. We could load the DPGA with assist functions, such as:

• ASCII decoding ( e.g. [Raz94])
• Bitvector manipulation
• Find first one ( e.g. [AS93])
• Hamming distance calculation ( e.g. [AS93])

Utility Functions

Some classes of functionality are needed, occasionally but not continuously. In conventional systems, to get the functionality at all, we have to dedicate wire or gate capacity to it, even though it may be used very infrequently. A variety of data loading and unloading tasks fit into this ``infrequent use'' category, including:

• Data offload
  • Debugging snapshot
  • Testing observability
  • Fault recovery snapshot
  • Context data offload
• Data onload
  • Configuration setting
  • Value initialization
  • Debugging value injection
  • Testing accessibility
  • Fault recovery
  • Context data reload (after coarse-grain context switch)
• Operation idle/enable
  • Conditional operation
  • Exception handling
  • Stall

In a multicontext DPGA, the resources to handle these infrequent cases can be relegated to a separate context, or contexts, from the ``normal'' case code. The wires and control required to shift in (out) data and load it are allocated for use only when the respective utility context is selected. The operative circuitry then, does not contend with the utility circuitry for wiring channels or switches, and the utility functions do not complicate the operative logic. In this manner, the utility functions can exist without increasing critical path delay during operation.

A relaxation algorithm, for instance, might operate as follows:

• Load in starting point and boundary conditions
• Calculate relaxation updates
• Check for convergence, return to 2 if not converged
• Offload result

Temporal Pipelining

In the introduction we noted that we can extract the highest capacity from our FPGAs by fully pipelining every operation. When we need the highest throughput for the task, but limited functionality, this technique works well. However, we noted in Section that application and technology bottlenecks often limited the rate at which we could provide new data for a design such that this maximum throughput is seldom necessary. Further, we noted that many applications are limited in the amount of distinct functionality they provide rather than the amount of throughput for a single function. Temporal pipelining is a stylized way of organizing designs for multi-context execution which uses available capacity to support a larger range of functions rather than providing more throughput for a single piece of functionality.

Temporally Systolic Pipelines

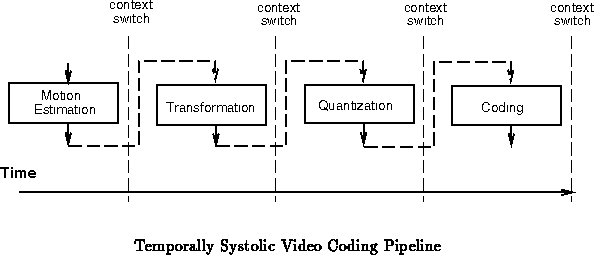
Figure shows a typical video coding pipeline ( e.g. [JOSV95]). In a conventional FPGA implementation, we would lay this pipeline out spatially, streaming data through the pipeline. If we needed the throughput capacity offered by the most heavily pipelined spatial implementation, that would be the design of choice. However, if we needed less throughput, the spatially pipelined version would require the same space while underutilizing the silicon. In this case, a DPGA implementation could stack the pipeline stages in time. The DPGA can execute a number of cycles on one pipeline function then switch to another context and execute a few cycles on the next pipeline function (See Figure ). In this manner, the lower throughput requirement could be translated directly into lower device requirements.

This is a general schema with broad application. The pipeline design style is quite familiar and can be readily adapted for multicontext implementation. The amount of temporal pipelining can be varied as throughput requirements change or technology advances. As silicon feature sizes shrink, primitive device bandwidth increases. Operations with fixed bandwidth requirements can increasingly be compressed into more temporal and less spatial evaluation.

When temporally pipelining functions, the data flowing between functional blocks can be transmitted in time rather than space. This saves routing resources by bringing the functionality to the data rather than routing the data to the required functional block. By packing more functions onto a chip, temporal pipelining can also help avoid component I/O bandwidth bottlenecks between function blocks.

Levelized Logic

Levelized logic is a CAD technique for automatic temporal pipelining of existing circuit netlists. Bhat refers to this as temporal partitioning in the context of the Dharma architecture [Bha93]. The basic idea is to assign an evaluation context to each gate so that:

• with a total ordering on contexts, all the inputs to context are computed in that context or one of its predecessors ( i.e. in a context such that )
• we minimize total capacity required for the calculation by minimizing the maximum resource usage per context

Figure shows a simple netlist with five logic elements. The critical path (ACE) is three elements long. Spatially implemented, this netlist evaluates a 5 gate function in 3 cycles using 5 physical gates. In three cycles, these five gates could have provided gate evaluations, so we realize a gate usage efficience, , of . The circuit can be fully levelized in one of two ways:

• = {A,B}, = {C}, = {D,E} (dashed lines in Figure )
• = {A}, = {B,C}, = {D,E}

The preceding example illustrates the kind of options available with levelization.

• Slack in the network allows us some freedom in the context placement for components outside of the critical path. In general, this slack should be used to equalize context size, minimizing capacity usage.
• Up to a point, more contexts allow increased utilization.
• Achieving the highest utilization often requires increasing the evaluation delay.

Table summarizes full levelization results for several MCNC benchmarks. sis [SSL +92] was used for technology independent optimization. Chortle [Fra92] [BFRV92] was used to map the circuits to 4-LUTs. For the purpose of comparison, circuits were mapped to minimize delay since this generally gave the highest, single context utilization efficiency. No modifications to the mapping and netlist generation were made for levelized computation. Gates were assigned to contexts using a list scheduling heuristic. Levelization results are not optimal, but demonstrate the basic opportunity for increased utilization efficiency offered by levelized logic evaluation.

full_wg_expl_long.tex

wire_vs_gate_opt.tex

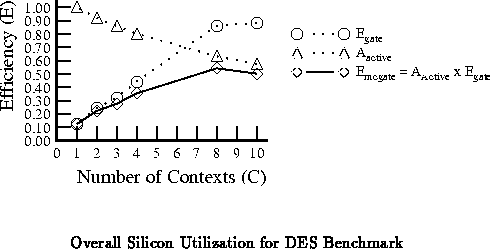
We saw in our simple example above that utilization efficiency varies with the number of contexts actually used. Table summarizes the gate efficiencies achieved for the DES benchmark for various numbers of contexts. The table also summarizes the utilization efficiency of the context memory (Equation ).

Figure plots both gate and memory utilization efficiency as a function of the number of contexts.

Recall from Section and Figure that context memory takes area away from active silicon. Figure combines the results from Table and Equation according to Equation to show the net silicon utilization efficiency for this design.

In this section we have focussed on cases where the entire circuit design is temporally pipelined. There are, of course, hybrids which involve some element of both spatial and temporal pipelining. An eight level deep piece of logic, for instance,

can be:

• fully spatially pipelined (operational bandwidth )
• broken into four spatial pipeline stages, each with two temporal stages (operational bandwidth )
• broken into two spatial pipeline stages, each with four temporal stages (operational bandwidth )
• fully temporally pipelined (operational bandwidth )

In general, once we have determined the level of spatial pipelining necessary to provide the requisite throughput, we are free to temporally pipeline logic evaluation within each spatial pipeline stage.

Finite State Machines

The performance of a finite state machine is dictated by its latency more than its bandwidth. Since the next state calculation must complete and be fed back to the input of the FSM before the next state behavior can begin, there is no benefit to be gained from spatial pipelining within the FSM logic. Temporal pipelining can be used within the FSM logic to increase gate and wire utilization.

Table summarizes the full levelization of several MCNC benchmark FSMs in the same style as Table .

Finite state machines, however, happen to have additional structure over random logic which can be exploited. In particular, one never needs the full FSM logic at any point in time. During any cycle, the logic from only one state is active. In a traditional FPGA, we have to implement all of this logic at once in order to get the full FSM functionality. With multiple contexts, each context need only contain a portion of the state graph. When the state transitions to a state whose logic resides in another context, we can switch contexts making a different portion of the FSM active. National Semiconductor, for example, exploits this feature in their multicontext programmable logic array (PLA), MAPL [Haw91].

In the most extreme case, each FSM state is assigned its own context. The next state computation simply selects the appropriate next context in which to operate. Table shows the reduction in logic depth and increase in utilization efficiency which results from multiple context implementation. FSMs were mapped using mustang [DMNSV88]. Logic minimization and LUT mapping were done with espresso, sis, and Chortle. All single context FSM implementations use one-hot state encodings since those uniformly offered the lowest latency and had the lowest capacity requirements. The multicontext FSM implementations use dense encodings so the state specification can directly serve as the context select. Delay and capacity are dictated by the logic required for the largest and slowest state.

Comparing Table to Table , we see that this state partitioning achieves higher efficiency gains and generally lower delays than levelization.

The capacity utilization and delay are often dictated by a few of the more complex states. It is often possible to reduce the number of contexts required without increasing the capacity required or increasing the delay. Table shows the cse benchmark partitioned into various numbers of contexts. These partitions were obtained by partitioning along mustang assigned state bits starting with a four bit state encoding. Figure plots the capacity and delay results from Table versus the number of contexts employed.

While demonstrated in the contexts of FSMs, the basic technique used here is also fairly general. When we can predict which portions of a netlist or circuit are needed at a given point in time, we can generate a more specialized design which only includes the required logic. The specialized design is often smaller and faster than the fully general design. With a multicontext component, we can use the contexts to hold many specialized variants of a design, selecting them as needed.

Conclusions

Programmable device capacity has both a spatial and a temporal aspect. Traditional FPGAs can only build up functionality in the spatial dimension. These FPGAs can only exploit the temporal aspect of capacity to deliver additional throughput for this spatially realized functionality. As a result, with heavy pipelining, FPGAs can provide very high throughput but only on a limited amount of functionality. In practice, however, we seldom want or need the fully pipelined throughput. Instead, we are often in need of more resources or can benefit from reducing total device count by consolidating more functionality onto fewer devices.

In contrast, DPGAs dedicate some on-chip area to hold multiple configurations. This allows resources such as gates, switches, and wires, to implement different functionality in time. Consequently, DPGAs can exploit both the temporal and the spatial aspects of capacity to provide increased functional capacity.

Fully exploiting the time-space capacity of these multicontext devices introduces new tradeoffs and raises new challenges for design and CAD. This paper reviewed several stylized models for exploiting the time-space capacity of devices. Multifunction devices, segregated utility functions, and temporally systolic pipelining are all design styles where the designer can exploit the fact that the device function can change in time. Levelized logic and FSM partitioning are CAD techniques for automatically exploiting the time-varying functionality of these devices. From the circuit benchmark suite, we see that 3-4x utilization improvements are regularly achievable. The FSM benchmarks show that even greater capacity improvements are possible when design behavior is naturally time varying. Techniques such as these make it moderately easy to exploit the wire and gate capacity improvements enabled by DPGAs.

See Also...

• PS Version of this note
• Accompanying slides [PS]
• DPGA Paper Index [HTML index]
• DPGA-coupled Processors (tn100) (tn118)

References

AS93

Peter Athanas and Harvey F. Silverman. Processor Reconfiguration Through Instruction-Set Metamorphosis. IEEE Computer, 26(3):11-18, March 1993.

BCE +94

Jeremy Brown, Derrick Chen, Ian Eslick, Edward Tau, and Andre DeHon. A 1 CMOS Dynamically Programmable Gate Array. Transit Note 112, MIT Artificial Intelligence Laboratory, November 1994. [tn112 HTML link] [tn112 PS link].

BCK93

Narasimha B. Bhat, Kamal Chaudhary, and Ernest S. Kuh. Performance-Oriented Fully Routable Dynamic Architecture for a Field Programmable Logic Device. UCB/ERL M93/42, University of California, Berkeley, June 1993.

BFRV92

Stephen D. Brown, Robert J. Francis, Jonathan Rose, and Zvonko G. Vranesic. Field-Programmable Gate Arrays. Kluwer Academic Publishers, 101 Philip Drive, Assinippi Park, Norwell, Massachusetts, 02061 USA, 1992.

Bha93

Narasimha B. Bhat. Novel Techniques for High Performance Field Programmable Logic Devices. UCB/ERL M93/80, University of California, Berkeley, November 1993.

BTA93

Jonathan Babb, Russell Tessier, and Anant Agarwal. Virtual Wires: Overcoming Pin Limitations in FPGA-based Logic Emulators. In Duncan A. Buell and Kenneth L. Pocek, editors, Proceedings of the IEEE Workshop on FPGAs for Custom Computing Machines, pages 142-151, Los Alamitos, California, April 1993. IEEE Computer Society, IEEE Computer Society Press.

CD96

Derrick Chen and Andre DeHon. TSFPGA: A Fine-Grain Reconfigurable Architecture with Time-Switched Interconnect. Transit Note 134, MIT Artificial Intelligence Laboratory, January 1996. [tn134 HTML link] [tn134 PS link].

DeH94a

Andre DeHon. DPGA-Coupled Microprocessors: Commodity ICs for the Early 21st Century. In Proceedings of the IEEE Workshop on FPGAs for Custom Computing Machines, April 1994. [FTP link].

DeH94b

Andre DeHon. DPGA-Coupled Microprocessors: Commodity ICs for the Early 21st Century. Transit Note 100, MIT Artificial Intelligence Laboratory, January 1994. [tn100 HTML link] [tn100 PS link].

DeH95

Andre DeHon. Notes on Coupling Processors with Reconfigurable Logic. Transit Note 118, MIT Artificial Intelligence Laboratory, March 1995. [tn118 HTML link] [tn118 PS link].

DMNSV88

Srinivas Devadas, Hi-Keung Ma, A.R. Newton, and Alberto Sangiovanni-Vincentelli. MUSTANG: State Assignment of Finite State Machines Targeting Multilevel Logic Implementations. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 7(12):1290-1300, December 1988.

Fra92

Robert Francis. Technology Mapping for Lookup-Table Based Field-Programmable Gate Arrays. PhD thesis, University of Toronto, 1992.

Haw91

David Hawley. Advanced PLD Architectures. In Will Moore and Wayne Luk, editors, FPGAs, pages 11-23. Abingdon EE&CS Books, 15 Harcourt Way, Abingdon, OX14 1NV, UK, 1991.

JOSV95

Chris Jones, John Oswald, Brian Schoner, and John Villasenor. Issues in Wireless Video Coding using Run-time-reconfigurable FPGAs. In Peter Athanas and Ken Pocek, editors, Proceedings of the IEEE Workshop on FPGAs for Custom Computing Machines, Los Alamitos, California, April 1995. IEEE Computer Society, IEEE Computer Society Press.

Raz94

Rahul Razdan. PRISC: Programmable Reduced Instruction Set Computers. PhD thesis, Harvard Univeristy, May 1994.

RS94

Rahul Razdan and Michael D. Smith. A High-Performance Microarchitecture with Hardware-Programmable Functional Units. In Proceedings of the 27th Annual International Symposium on Microarchitecture, pages 172-180. IEEE Computer Society, November 1994.

RSV87

R. Rudell and A. Sangiovanni-Vincentelli. Multiple-Valued Minimization for PLA Optimization. IEEE Transactions on Computer-Aided Design of Integrated Circuits, 6(5):727-751, September 1987.

SSL +92

Ellen M. Sentovich, Kanwar Jit Singh, Luciano Lavagno, Cho Moon, Rajeev Murgai, Alexander Saldanha, Hamid Savoj, Paul R. Stephan, Robert K. Brayton, and Alberto Sangiovanni-Vincentelli. SIS: A System for Sequential Circuit Synthesis. UCB/ERL M92/41, University of California, Berkeley, Department of Electrical Engineering and Computer Science, University of California, Berkeley, CA 94720, May 1992.

TEC +95a

Edward Tau, Ian Eslick, Derrick Chen, Jeremy Brown, and Andre DeHon. A First Generation DPGA Implementation. In Proceedings of the Third Canadian Workshop on Field-Programmable Devices, pages 138-143, May 1995. [FTP link].

TEC +95b

Edward Tau, Ian Eslick, Derrick Chen, Jeremy Brown, and Andre DeHon. A First Generation DPGA Implementation. Transit Note 114, MIT Artificial Intelligence Laboratory, January 1995. [tn114 HTML link] [tn114 PS link].

WH95

Michael J. Wirthlin and Brad L. Hutchings. A Dynamic Instruction Set Computer. In Peter Athanas and Ken Pocek, editors, Proceedings of the IEEE Workshop on FPGAs for Custom Computing Machines, Los Alamitos, California, April 1995. IEEE Computer Society, IEEE Computer Society Press.

Xil94

Xilinx, Inc., 2100 Logic Drive, San Jose, CA 95124. The Programmable Logic Data Book, 1989, 1994.

Memory Technology

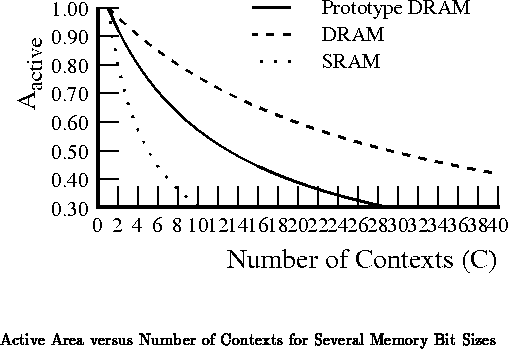
In Section and Figure we saw how active capacity varied with the number of supported contexts. In Section , we took technology numbers from the DPGA prototype. The exact shape of the curves, or more particularly, the in Equation , depends on the memory bit density. In this section we show this same data for two other, relevant, memory densities.

Denser DRAM

As noted in [TEC +95a], the DPGA prototype used a DRAM cell with a particularly asymmetric aspect ratio which made it a factor of two larger than it could have been: 146 vs 75. Using the tighter DRAM, we could have placed 8 contexts in the same space as the prototype. Solving Equation at this point gives: .

SRAM

An SRAM cell would have required 300 per bit instead of 146. To first order, we could have placed only 2 contexts in the same space as the prototype context memory. In practice, the SRAM cells would remove the need for the refresh control circuitry such that the actual area difference would be smaller than this factor of two implies. Solving Equation assuming only two contexts gives .

Figure plots these three curves together to show the difference made by these various memory bit densities.

Density v/s Diversity Tradeoff

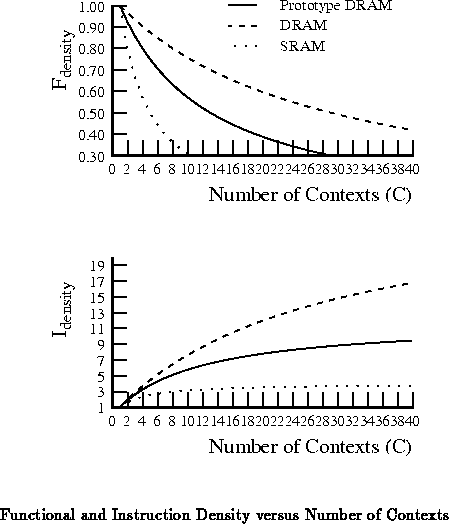
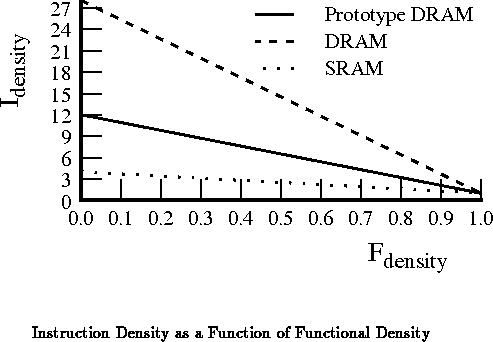
The tradeoff we are making when we add more context memory is to decrease the density of active computional elements, functional density, in order to increase the density of diverse operations, instruction density or functional diversity. Figure plots both functional density and the instruction density against the number of contexts for the memory densities of the previous section. Figure plots functional density versus instruction density.

Context Memory Read Overhead

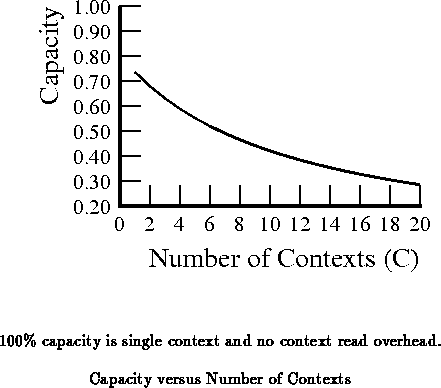
In Section , we also noted that the time taken to read context memory introduces a delay which increases , reducing delivered capacity. Reviewing the DPGA prototype times, without a context switch is roughly 7 ns when it includes one LUT evaluation and one crossbar traversal. The context read adds 2.5 ns to the cycle time. The result is a 26% capacity loss. Figure replots Figure in terms of capacity to show this effect.

Gate Through Levelization

In the DPGA prototype (tn112) (tn114), the only way to route a signal through a context is via a logic block. The inputs to a context are limited to the logic and input block flip-flop outputs. In general, the logic block flip flops are used to communicate results from one context to the next. As a consequence, if a value produced in context is consumed at context and , a logic block with associated flip flop must be allocated to route that signal through each of the intervening contexts (,,...,).

For example, let us reconsider Figure in light of this restriction. Using the partitioning shown in the figure and assuming the inputs to the example come from the I/O pins, the middle stage would require two logic blocks:

• one to implement block C
• one to route the output of B from the previous context to the succeeding context

With this additional constraint, is is necessary to include the through routing in with the number of gates occupied at a particular level. This produces a different optimization criteria and efficiency metric. During levelization, we are now minimizing the sum of the through connections and gate utilization in the most heavily used context. Efficiency, in this case, is defined as:

Table parallels Table , showing the efficiencies achieved under this model. As before, the results for each circuit shown in Figure represent a different levelization than the ones in Table . As we expect, the need to dedicate logic blocks for through traffic decreases the efficiencies achieved.

Figure shows the capacity and efficiency for the DES benchmark as a function of the number of contexts. We see a less graceful degradation in efficiency under this gate through model.

Under the pure gate and wire models it was theoretically possible to achieve 100% efficiency by adding sufficient levels to balance the contexts. In the extreme, for example, one can evaluate a single gate per context until the entire circuit is evaluated. This is not the case under this model. The through routing only increases as the number of contexts are increased beyond the number of topologically required levels.

Dharma [BCK93] dedicated separate buffer resources for through routing. As a consequence Dharma does not, necessarily, consume gates for through routing. However, this means Dharma has staticly designed in two different kinds of resources for evaluation and made a static partition of interconnect resources between these two functions. Since both approaches have their benefits and drawbacks, it is not immediately clear which is preferable.

It is likely that there is a better alternative than either. For example, it might be worthwhile to create some inter-context ``long lines''. Somewhat like ``long lines'' in conventional FPGAs, these would span multiple contexts rather than spanning multiple rows or columns of array elements. Resources to ``park'' through connections might also be beneficial. Here, we might allocate a place to store and then recover values which are needed at a later time; this is the approach taken in TSFPGA (tn134).

The netlists input to the levelization process were not specifically targeted for levelized computation. Introducing the through routing costs at the network generation level may allow us to produce networks more amenable to efficient levelization.

This is one area which merits attention in the further development of this technology. The combination of the current DPGA routing architecture with the off-the-shelf netlist generation is not extracting as efficient results as appear possible.