
Transit Note #113
Specialization versus Configuration
Andre DeHon
Original Issue: January, 1995
Last Updated: Fri Jan 13 18:13:26 EST 1995

Abstract:
Exploiting the full potential of reconfigurable computing devices requires
a different design style than that normally employed for fixed computing
devices. To achieve adequate flexibility, fixed computing devices such as
ASICs or microprocessors, can be configured to adapt their behavior
to match the needs of a particular application. While this configurability
costs performance and area, it is generally necessary so that a single
design can achieve wide-spread applicability. With reconfigurable
computing devices, however, the fact that the whole device can be
configured on a per application and per use basis means that reconfigurable
designs can be specialized to the behavior required rather than
configured. The reconfigurable architect, therefore, needs to more
carefully consider the binding time for various parameters in the logic
design and exploit the fact that many parameters are known prior to an
operational epoch and will remain constant throughout use.
Introduction
One of the key advantages of a run-time customizable compute engine, or any
reprogrammable function block in a design, is that we can specialize the
compute engine to closely match the needs of the application. That is, the
run-time reconfigurability allows us to focus on solving only the
particular problem at hand. We can thus freely discard any functionality
and options which might be needed by a computing device solving a more
general problem, but are not presently needed for performing the
computation currently required. This characteristic creates opportunities
for optimization in reconfigurable designs which are not viable for
fixed-logic designs.
Consider, for example, a typical UART. A conventional, hardwired UART can be
configured to operate with 5-8 character bits, with or without parity, and
with programmable divide counters. The device must additionally provide an
interface for loading configurations. This configurability must be built
into the UART for two reasons: (1) to assure that the device will appeal to
a large portion of the market, and (2) so that a single device can service
the wide range of potential uses required by the end user.
However, all of the UART configuration options, character width, parity
scheme, and clock division amount, are constant throughout any single
communication session. A reconfigurable UART design benefits
from folding these constants into the design logic rather than mimicking
the ASIC design which incorporates run-time logic structures
which allow these values to change.
In general, a key difference between fixed logic designs and reconfigurable
logic designs is the binding time for the logic netlist. Fixed logic
functions must be bound prior to fabrication and distribution. Since IC
fabrication is both time consuming and expensive, the fixed logic design
bound into the device at fabrication time must be generic enough to appeal
to a wide market and be useful for the lifetime of end applications. The
function performed by a reconfigurable logic design, however, need not be
bound until loaded into the reconfigurable logic device. At this point it
need only be generic enough to operate until reloaded -- or, more
precisely, it only need to be generic enough that reload requirements do
not preclude proper operation or detract from design performance.
In this paper we review the advantages of design specialization across a
set of example subcircuits and comment on the way architects should employ
specialization in reconfigurable designs. We start off in
Section  by summarizing a collection of specialization
experiments. We follow the summary up by highlighting a few other
specializations which have been used in contemporary reconfigurable designs
in Section
by summarizing a collection of specialization
experiments. We follow the summary up by highlighting a few other
specializations which have been used in contemporary reconfigurable designs
in Section  . In Section
. In Section  we discuss the
benefits of specialization, and in Section
we discuss the
benefits of specialization, and in Section  we discuss when it is
advantageous to specialize.
we discuss when it is
advantageous to specialize.
Specialization Experiments

In this section, we report on a series of experiments aimed at providing
a rough characterization of the effects of specialization. We break the
experiment into three pieces: simple logic subcircuits, finite-state
machines, and composite designs.
Basic Framework
For all these experiments, we started with the generic function described
in an RTL-level hardware-description language. Designs were synthesized
down to FPGA logic netlists using the Synopsys Design Compiler
[Syn92] with FPGA
vendor design libraries. Where applicable the designs were synthesized
separately to minimize area and to minimize latency. In many cases where
this did not generate distinct and interesting mapped logic points, only a
single mapped point is reported.
Since the goal was primarily to generate a comparison between generic and
specialized instances of a design, the designs were synthesized and
optimized to generate mapped logic netlists but not run through back-end
place and route. Additionally, since many of the designs here are
sub-circuits which would not stand-alone, it would be difficult to get
meaningful, post routing results for comparison. The mapped results
included here are reported with size and delays given in terms of basic
logic blocks. Experience suggests that routed delay will be affected by
both the critical path delay shown and the total size of the mapped logic.
To generate specialized derivatives of designs, appropriate values in the
design were hardwired to constants before synthesis. Where feasible, the
space of possible constants was tested. In other cases, constants were
judiciously chosen in an attempt to elicit the worst-case size and speed
results and to characterize the space of specializations.
For brevity, we primarily report the results of synthesizing to the
Xilinx 4000 [Xil93] family of FPGAs. For most of the cases
reported here, we also synthesized to the Altera Flex 8000 [Alt93]
family and Actel Act2 [Act90] family to convince ourselves that the
results were not artifacts of the Xilinx architecture. Comparable results
were achieved across all architectures targeted.
Logic Subcircuits
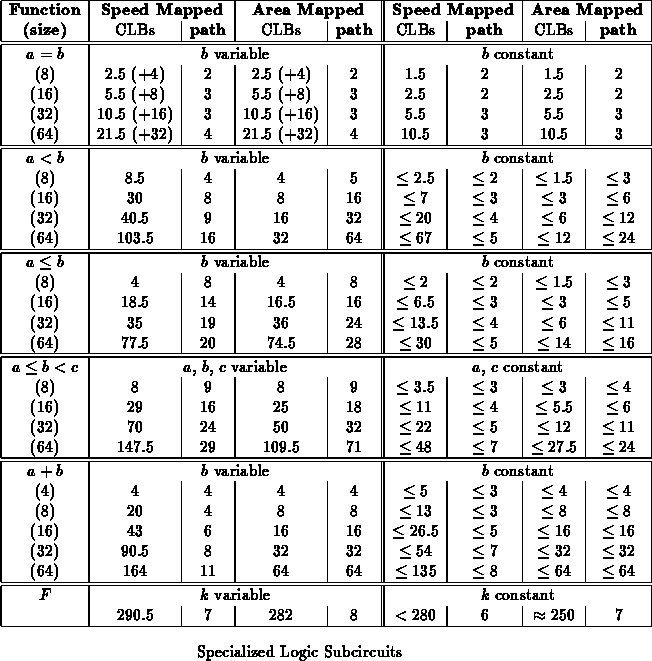
Table  summarizes specialization results for a number
of logic circuits. For each function, several sizes of operation are
given, as well as the worst-case size and speed across the specialized
values. In general, the specialized instances have a slightly shorter
critical path while requiring significantly less area.
summarizes specialization results for a number
of logic circuits. For each function, several sizes of operation are
given, as well as the worst-case size and speed across the specialized
values. In general, the specialized instances have a slightly shorter
critical path while requiring significantly less area.


Sizes
Often it is the case that a specialized piece of logic
can work with a reduced data size. For example, if the operands into an
adder are known to be less than 32, we need only use a 5-bit adder.
Similarly, if the low  -bits of an operand to an
-bits of an operand to an  -bit adder are known to
be zero, the adder can be reduced to an
-bit adder are known to
be zero, the adder can be reduced to an  bit adder. In some cases, a
single operand may be known to be small while the other may be larger.
Here, an asymmetric, specialized adder can be built which feeds in constant
zeros to the high bits of the adder for the small operand. One of the
reasons for including several different sizes in Table
bit adder. In some cases, a
single operand may be known to be small while the other may be larger.
Here, an asymmetric, specialized adder can be built which feeds in constant
zeros to the high bits of the adder for the small operand. One of the
reasons for including several different sizes in Table  is to show the savings available when a reduced-size operation can be
substitute for a more generic operation.
is to show the savings available when a reduced-size operation can be
substitute for a more generic operation.
Configuration Registers
The table shows the sizes for the
logic itself without charging space for the configuration registers
which may be necessary to hold the comparison operand in the generic case.
The table entry for equal shows the additional area required for a minimal
configuration register in parenthesis to put in perspective the size
required to accommodate this logic. For example, a 16-bit comparator
requires 13.5 CLBs if a 16-bit register is required to hold the comparison
target. Recall that Xilinx CLBs each house a pair of output bits including
4-LUTs and optional flip-flops associated with each output, hence we expect
it to require one CLB for each pair of configuration bits as shown. The
rest of the entries omit listing this cost since the cost is not effected
by the designs themselves.
Addition
The area results for addition are somewhat anomalous
in that there are bad input cases in which the specialized logic does not
come out smaller than the generic case. This seems to be more an artifact
of the optimization tools than a true exception. We can hand map any
 -bit add to any
-bit add to any  -bit constant into
-bit constant into  4-input
lookup tables with a critical path delay of
4-input
lookup tables with a critical path delay of  .
This mapping occurs by breaking the problem into 3-bit slices. Each output
bit is computed from the 3 data input bits to the 3-bit slice plus the
carry in to the 3-bit slice. A fourth cell in the 3-bit slice computes the
carry out of this slice to the next one. Since Xilinx places two 4-input
lookup tables per CLB, the
.
This mapping occurs by breaking the problem into 3-bit slices. Each output
bit is computed from the 3 data input bits to the 3-bit slice plus the
carry in to the 3-bit slice. A fourth cell in the 3-bit slice computes the
carry out of this slice to the next one. Since Xilinx places two 4-input
lookup tables per CLB, the  -bit add to constant can be done in
-bit add to constant can be done in
 CLBs. Using 4-input lookup tables, the minimum
size for a generic
CLBs. Using 4-input lookup tables, the minimum
size for a generic  -bit add is
-bit add is  lookup tables or
lookup tables or  CLBs with a
critical path length of
CLBs with a
critical path length of  as indicated in the Table
as indicated in the Table  .
.
Anyone who has used the Xilinx 4000 series extensively will note that the
results shown in Table  are larger and slower than
typical Xilinx adders. The synthesis tools did not map to the specialized
carry logic available on the Xilinx array. Early Xilinx software only
exported this feature through its adder hard macro so the carry resource
can only be employed when custom adder blocks are inserted in the design
and not when the adder function is being inferred from logic. Using the
fast carry support, an
are larger and slower than
typical Xilinx adders. The synthesis tools did not map to the specialized
carry logic available on the Xilinx array. Early Xilinx software only
exported this feature through its adder hard macro so the carry resource
can only be employed when custom adder blocks are inserted in the design
and not when the adder function is being inferred from logic. Using the
fast carry support, an  -bit adder can be implemented in
-bit adder can be implemented in
 CLBs [Xil93].
CLBs [Xil93].
DES F Function
The F function which forms the kernel of the DES [Nat77]
algorithm takes a 32-bit data input and a 48-bit key input to generate a
32-bit output. The F function includes an expansion of the input, an
XOR with the key, lookup through 8 S-boxes and a permutation of the output
bits. This is one example where the payoff of specialization is
negligible. Since the key is XOR'd with the expanded data, the
output of the XOR can still take on any input value. The
specialization only succeeds in removing the XOR stage and very
little of the encoding logic.
Finite State Machine Examples
Table  summarizes several finite-state machine designs which can
be specialized around various configurations.
summarizes several finite-state machine designs which can
be specialized around various configurations.
- METRO forward -- METRO is a self-routing, dilated,
pipelined, crossbar routing component [DCB +94]. This FSM
interprets signaling on the incoming link and arbitrates for output
connections through the crossbar.
- MLINK node i/o -- MLINK is an interface between a host
node and a METRO network [DeH93b]. The node i/o
operation handles autonomous block data transfer between the node's
memory and the MLINK component.
- MLINK central -- The central state machine is the master
controller responsible for MLINK operation including link
signaling, packet formation, and status and error handling.
- I8251 processor i/o -- Intel's 8251 is a programmable USART
[Int89]. This FSM handles control for
read/write operations from the processor port including configuration
loading, status reads, and data read/write operations.
- I8251 transmitter -- The transmitter FSM handles outgoing
data signaling for the USART, shipping parallel data out serially according
to the selected configuration.
- I8251 receiver -- The receiver FSM handles incoming
data signaling for the USART, interpreting the input stream and turning it
into parallel data according to the programmed configuration.



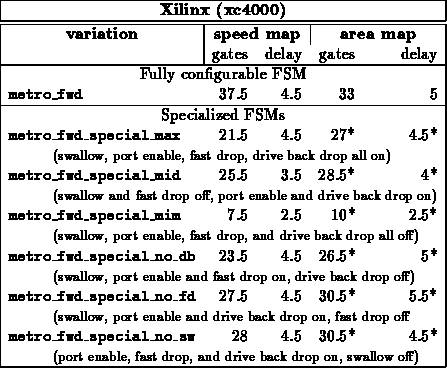
For all cases, we see a significant area savings and a slight reduction in
critical path length by specializing to the particular configuration.
In all cases, reducing the number of inputs affecting FSM behavior
simplifies the logic. Some states are reachable only in select
configurations, so specialization often reduces the number of states
handled by the state machine.
Composite Designs
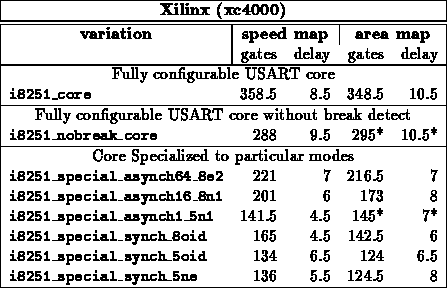
Table  summarizes specializations for the core of
METROJR and the core of an I8251 USART. Both designs include all the core
logic up to, but not including, i/o pads. Both design include a mix of
FSMs, control logic, and datapaths.
summarizes specializations for the core of
METROJR and the core of an I8251 USART. Both designs include all the core
logic up to, but not including, i/o pads. Both design include a mix of
FSMs, control logic, and datapaths.



METROJR
A reasonable amount of area on the
METROJR design goes into configuration registers and scan support to load
the configuration registers. Specializing the configured values
immediately allows one to dispense with the configuration support
circuitry.
I8251
The behavior of the USART differs significantly between
synchronous and asynchronous mode. By specializing the design to a single
configuration, the unnecessary support can be removed from the design.
Further, in cases where the character size is reduced or the programmable
division rate is reduced, high bits of the datapath and counters become
unused and can be discarded, as well.
Specialization Highlights

There are a number of spot examples of this genre of specialization for
reconfigurable logic designs in the literature. Here we highlight three to
fill out the picture.
Multiplier Specialization
EDN's 1993 Design Idea winner was a
specialized multiplier [Cha93]. The  multiplication was effectively performed by looking up the 12-bit result of
each 4-bit
multiplication was effectively performed by looking up the 12-bit result of
each 4-bit  8-bit partial product in a
8-bit partial product in a  lookup table
preloaded with all 16 possible 12-bit product results obtainable by
multiplying a 4-bit value by an 8-bit constant. A single 16-bit adder
combines the two partial products into a full product. The design is thus
specialized to multiply by a constant. Since the multiplier is trivially a
lookup table, Chapman also details circuitry to recalculate and reload the
lookup table in case the specialized operand needs to change.
lookup table
preloaded with all 16 possible 12-bit product results obtainable by
multiplying a 4-bit value by an 8-bit constant. A single 16-bit adder
combines the two partial products into a full product. The design is thus
specialized to multiply by a constant. Since the multiplier is trivially a
lookup table, Chapman also details circuitry to recalculate and reload the
lookup table in case the specialized operand needs to change.
Modulus Specialization
In their implementation of modular multiplication on PAM
[SBV91], the multiplier operation is specialized around
the multiplication modulus.
FIR Filter
Mitzner introduces an FIR Filter architecture for
FPGAs [Min93] designed to specialize the tap filter coefficients
into the array product generation. The filter inputs are presented in bit
serial fashion to a lookup table such that the lookup table sees the
 -th input bit from each of the
-th input bit from each of the  inputs on the
inputs on the  -th cycle of
operation. The lookup table, preloaded according to the coefficient set,
generates a partial sum for each set of input bits. The sum is shifted and
added by an output accumulator to generate the desired filter value. By
specializing the coefficients into the lookup table, input scaling and
addition is handled simultaneously requiring only a single series of
-th cycle of
operation. The lookup table, preloaded according to the coefficient set,
generates a partial sum for each set of input bits. The sum is shifted and
added by an output accumulator to generate the desired filter value. By
specializing the coefficients into the lookup table, input scaling and
addition is handled simultaneously requiring only a single series of  lookups and adds to generate the complete sum.
lookups and adds to generate the complete sum.
Benefits of Specialization

As the previous sections demonstrate, specialization yields smaller and
faster designs that provide the required functionality in restricted
operational domains.
Space Savings
Since the specialized logic is generally much more compact than its
generic counterpart, specialization may make it possible to fit designs
into available logic area when the generic design will not fit. For
example, the savings due to specialization in the METROJR case might
allow it to fit in the next smaller Xilinx array.
Alternately, specialized designs may allow more functionality to be
packed into the available space. Two specialized UARTs may be able to fit
in the space of a single generic UART. Further, space savings from
specialization may allow other resources in the design to expand to exploit
the additional space. For example, in a communication device, input or
output FIFOs can be expanded as space permits.
Size Variation
The size of a specialized instance is often data dependent.
Multiplication by zero, or a power of two, for instance, requires no logic
while other constants require more complicated logic. In the same vein, as
suggested above, sometimes it is possible to work with reduced data sizes,
reducing operator size. This raises the issue of whether or not the
additional benefit of a favorable data pattern is exploitable? I.e.
is the maximum specialized size across all data values the only one of
interest?
In some case, the maximum may be all that matters. If you only have a
fixed amount of room for the design, you need to make sure all possible
specializations will fit. For example, when picking an FPGA array on which
to implement a specialized METROJR, it is necessary that the FPGA
accommodate the largest, specialized configuration which may be needed. Of
course, one may decide that certain configurations are undesirable simply
because they require excessive space and consequently find ways to avoid
those specializations.
In some cases, the design will include resources which are mutually
exclusively. For the MLINK node i/o FSM, the ``zero dummy cycles''
case is half-again the size of the ``programmed dummy cycles case.''
However, in full MLINK component, the ``programmed dummy cycles''
case also requires a counter to count dummy cycles whereas no such
counter is needed in the ``zero dummy cycles'' case.
Often a design can be parameterized such that the amount of hardware
instantiated can be adapted to the available space. Specialized instances
may allow more functionality to be realized than with generic designs.
When favorable specialization patterns allow more compact instances, more
instances can be instantiated to exploit the available area.
Performance Improvement
Direct performance improvement through critical path reduction is
generally slight as indicated in Section  . Nonetheless,
the specialized designs are generally faster than the speed mapped generic
design while being smaller than the area mapped generic design. Further,
routed delays are likely to display a greater savings for the smaller,
specialized design.
. Nonetheless,
the specialized designs are generally faster than the speed mapped generic
design while being smaller than the area mapped generic design. Further,
routed delays are likely to display a greater savings for the smaller,
specialized design.
As with spatial usage, the performance of a specialized circuit is often
dependent on the specialized values, and the extent to which favorable
timings can be exploited depends on the usage scenario. If a specialized
component is out of the critical path, its performance improvement will not
bear on the design. If it is on the critical path, but the timing for the
design must be static across all specializations, the worst-case,
specialized delay will set the operational speed. However, if the timing
on the design can be adjusted to exploit the timing possible with each
particular specialization, we can extract increased performance when a
favorable specialized instance is used. In a high-speed, clocked scenario,
the variable timing can be accommodated by allowing the design an
appropriate number of clock cycles to complete based on the specialization
employed. Finally, within a composite design, timing is often
complementary. That is, the slow patterns for one sub circuit may
correspond to the fast patterns for a dependent circuit. In all cases, the
performance of the composite design is what really matters.
Finding Opportunities for Specialization

Operational Parameters
The most obvious candidates for specialization are cases where the
configuration is static across long operational epochs. Gross
configuration behavior as suggested above for the router, network
interface, UART, or filter are clear examples where specialization should
be employed in reconfigurable designs.
Slowly Changing Values
However, specialization may also be beneficial any time when
some portion of the data in a computation changes slowly
compared to the rest of the data being processed by the computation.
For example, a search through a large database might benefit from using a
specialized detection circuit tailored to the search target rather than
using a generic comparator configured with the search target. Similarly, a
commonly used bounds check who's range changes infrequently might be
specialized around the selected bound. Multiplication and addition
operations where one operator changes much more slowly than the other may
merit similar specialization.
This class of specializations is directly analogous to the run-time
generation of specialized machine code and can be one of the key strengths
for reconfigurable computing logic. Regular expression searches, for
example, have often tended to compile matching code at run-time to generate
highly efficient search code tailored to the target expression
[Tho68]. In a similar manner, a hardware pattern matcher
can be specialized at run-time to the pattern of interest, yielding a
leaner and faster hardware matching implementation.
One key factor determining the beneficial application of specialization
is the time it takes to acquire and install a new configuration for the
programmable machines. Certainly, when configurations must be reloaded
during operation, in order for the specialization to be beneficial, the
specialized logic must run sufficiently faster than the non-specialized one
to offset the costs of a reload operation.
The cost of acquiring a new specialization can vary widely:
- New specializations may take 10's of minutes to compute,
requiring processing by synthesis, placement, and routing tools.
- Reloading conventional FPGAs takes 10's of milliseconds once an
available configuration exists.
- Swapping to a loaded configuration on a DPGA design [BDK93]
[DeH94] can occur in 10's of nanoseconds.
In cases where the number of desired specializations is small, it will be
beneficial to precompute the specialized logic and store it on disk or
Flash ROM so that it can be loaded quickly as needed. In cases where the
specialization space is large, it may not be feasible to compute all
possible specializations in advance or worthwhile to store the routed
designs. A simple scheme would be to store a generic design along with the
stored specializations. Whenever a specialized instance is applicable, the
system can use the specialization if it exists and the generic case
otherwise. In either case, the value of the requested specialization is
noted. During idle time the host system can then make use of the
specialization usage statistics to determine which new specializations it
should generate and which specializations it should prune when storage
space is limited. In some cases it may be worthwhile to take the time to
generate the new specialization on the fly rather than use an unspecialized
design. This will certainly be true for specializations which will be used
for large computing epochs or provide significant speed advantages over
their generalized counterparts.
Conclusions

Efficient architectures targeted for reconfigurable computing differ from
conventional architectures employed for fixed logic components. In
particular, the later binding time associated with reconfigurable logic
netlists give the reconfigurable architect the opportunity to specialize
his design more precisely to the particular use to which the device will be
employed during an operational epoch. This specialization can result in
large reductions in the size of a design. Further, the specialization can
increase the performance of the design both directly, by lowering the
critical path length of the circuit, and indirectly, by allowing more
functionality to be employed in the limited space available for
reconfigurable compute logic. Consequently, the reconfigurable architect
needs to pay careful attention to the binding time of values in the
applications he designs. Values bound early and changing infrequently
present opportunities to benefit from specialized designs.
See Also...
References
- Act90
-
Actel Corporation, 955 East Arques Avenue, Sunnyvale, CA 94086.
ACT 2 Field Programmable Gate Array, 1990.
- Alt93
-
Altera Corporation, 2619 Orchard Parkway, San Jose, CA 95314-2020.
Data Book, August 1993.
- BDK93
-
Michael Bolotski, Andre DeHon, and Thomas F. Knight Jr.
Unifying FPGAs and SIMD Arrays.
Transit Note 95, MIT Artificial Intelligence Laboratory, September
1993.
[tn95 HTML link] [tn95 FTP link].
- Cha93
-
Kenneth David Chapman.
Fast Integer Multipliers fit in FPGAs.
EDN, 39(10):80, May 12 1993.
- DCB +93
-
Andre DeHon, Frederic Chong, Matthew Becker, Eran Egozy, Henry Minsky, Samuel
Peretz, and Thomas F. Knight, Jr.
METRO: A Router Architecture for High-Performance, Short-Haul
Routing Networks.
Transit Note 96, MIT Artificial Intelligence Laboratory, September
1993.
[tn96 HTML link] [tn96 FTP link].
- DCB +94
-
Andre DeHon, Frederic Chong, Matthew Becker, Eran Egozy, Henry Minsky, Samuel
Peretz, and Thomas F. Knight, Jr.
METRO: A Router Architecture for High-Performance, Short-Haul
Routing Networks.
In Proceedings of the International Symposium on Computer
Architecture, pages 266-277, May 1994.
[FTP link].
- DeH92
-
Andre DeHon.
METRO LINK -- METRO Network Interface.
Transit Note 75, MIT Artificial Intelligence Laboratory, September
1992.
[tn75 HTML link] [tn75 FTP link].
- DeH93a
-
Andre DeHon.
METRO LINK Programmer's Quick Reference.
Transit Note 81, MIT Artificial Intelligence Laboratory, March 1993.
[tn81 HTML link] [tn81 FTP link].
- DeH93b
-
Andre DeHon.
Robust, High-Speed Network Design for Large-Scale Multiprocessing.
AI Technical Report 1445, MIT Artificial Intelligence Laboratory,
545 Technology Sq., Cambridge, MA 02139, February 1993.
[AITR-1445 FTP link].
- DeH94
-
Andre DeHon.
DPGA-Coupled Microprocessors: Commodity ICs for the Early 21st
Century.
In Proceedings of the IEEE Workshop on FPGAs for Custom
Computing Machines, 1994.
[FTP link].
- Int89
-
Intel Corporation, 3065 Bowers Avenue, Santa Clara, CA 95051.
Microcommunications Handbook, 1989.
- Min93
-
Les Mintzer.
FIR Filters with Field-Programmable Gate Arrays.
Journal of VLSI Signal Processing, 6:119-127, 1993.
- Nat77
-
National Bureau of Standards, Washington, DC.
Data Encryption Standard, January 1977.
FIPS PUB 46.
- SBV91
-
Mark Shand, Patrice Bertin, and Jean Vuillemin.
Hardware Speedups in Long Integer Multiplication.
Computer Architecture News, 19(1):106-114, 1991.
- Syn92
-
Synopsys.
Design Compiler Reference Manual.
Synopsys, Inc., version 3.0 edition, December 1992.
- Tho68
-
Ken Thompson.
Regular Expression Search Algorithm.
Communications of the ACM, 11(6):419-422, June 1968.
- Xil93
-
Xilinx, Inc., 2100 Logic Drive, San Jose, CA 95124.
The Programmable Logic Data Book, 1993.
Detailed Results
This appendix contains more detailed tables which summarize the results of
various specializaiton expriements.
Note, the main paper primarily reported the results for the Xilinx 4000
series devices. In several cases the experiments were also run for Actel
Act2 and Altera Flex 8000 devices to increase confidence that the xc4000
results were typical. Where the specializations were run, that data is
included here.
For all tests --
- Path lengths (path) are given in units of gate delays (logic
blocks in longest paths).
- In synchronous designs, the initial
 time is
counted as half a gate-delay.
time is
counted as half a gate-delay.
- In all cases synthesized for both minimal speed and minimal area.
In some cases, the minimum area/speed synthesis case turned out to
be larger than the area/speed in the synthesis with the opposite
goal. These cases are generally marked with an asterisk.
- Also marked are cases which don't fit into bracketted progression
-- these cases are likely to be ones where the synthesis tool
gave up before finding the same optimizations as the
bracketting cases.
Some thing I've noticed unfortunately after running everything through
once:
- If I just synthesize for speed across all constants, then look at
the results, I can find the fastest I can run all of the
constants -- but, that, alone doesn't give me the area associated
with that speed. That is, in some cases it will be able to run
faster and, consequently, consume more area. So the maximum area
associated with the set of ``fastest'' designs seldom corresponds
to running at the speed marked fastests (usually its at a faster
speed). So, if you want a single fast/area bound for a set of
constant specializations, you have to synthesize through in two
steps (1) find fastest can run all of them then and (2) set a time
bound and synthesize everything to that time bound.
- When Synopsys gives up on an optimization, it doesn't give you the
best time/area pair -- just the last. So, if it's optimizing for
timing, it may go through some passes where it increases the area
but not the speed. If it fails to increase the speed any further
it does not go back to the smallest design at the acquired
speed. The solution here is as above -- you need to first find the
best achievable target speed then resynthesize to that speed target
to find the minimum area associated with the best achievable speed.
I've tried to chase down the major places where these effects have produced
overly pessimistic results, but there may still be some cruft as a result.
Equal ( )
)
- For this test, all constant values were effectively tested.
- Numbers shown in parenthesis are the additional cells required
for a configuration register to hold the value of
 .
.
- Delays are for path through logic (
 ).
).
 on the configuration registers are not included.
on the configuration registers are not included.

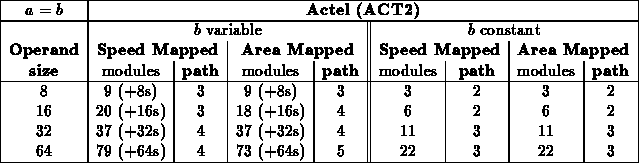
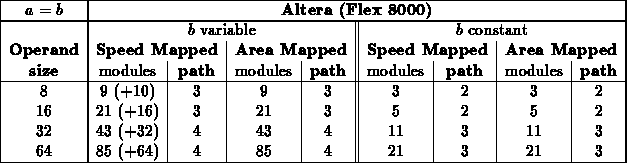
It makes sense that ( ) is indepdendent of constant
value. The logic breaks down to:
) is indepdendent of constant
value. The logic breaks down to:

With the constant  known,
known,  becomes either
becomes either
 or
or  . The presence or absence of the inversion on
. The presence or absence of the inversion on
 is irrelevant for most FPGA technologies since the polarity inversion
can almost always be folded into the primitive logic cells at no additional
cost in logic.
is irrelevant for most FPGA technologies since the polarity inversion
can almost always be folded into the primitive logic cells at no additional
cost in logic.
The size and results also match expectations. Here, we are essentially
eliminating one op, the XNOR, at the leaf of a balanced computational
tree. We save the single gate delay for the leaf computation, but still
have to build the entire tree to compute the large fan-in AND.
Since we are looking at a balanced tree fan-in, simply eliminating the leaf
level will easily save us one-half to three-fourths of the total tree size,
depending on the branching factor at the leaf.
The leaf branching factor explains why we see the difference in
assymptotic benefit between the Xilinx arrays and the Actel/Altera arrays.
In the Xilinx case, each primitive element (half a CLB) is a 4-LUT and can
implement any function of 4 inputs, it can, thus, implement two
XNOR's followed by a combining AND. The Actel/Altera cells have a
finer grain structure that cannot implement arbitrary 4-input functions.
Each XNOR requres a single module. However, all three technologies
can implement a variety of 4-input AND functions in a single level.
The Xilinx thus sees a branching factor of 2 at the leaves, and hence a
savings of one-half, while the Actel/Altera see a branching factor of 4
and, savings of three-fourths.
Less Than ( )
)
- For this test, a scattered sampling of values where used (results
could reflect some bias on value choices): 0x8(0), 0x7(F),
0x4(0), 0x3(F), 0x7(7), 0x7(0), 0x3(3), 0x3(0), 0x1(1), 0x1(0)
[Number in parentheses repeated to fill out number to comparator
size.]
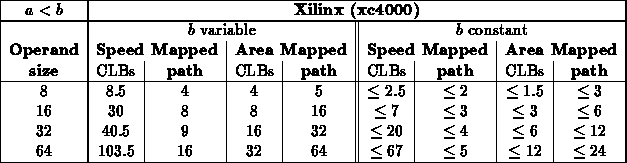
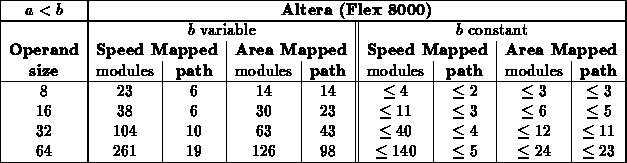
Less Than or Equal ( )
)
- For this test, a scattered sampling of values where used (results
could reflect some bias on value choices): 0x8(0), 0x7(F),
0x4(0), 0x3(F), 0x7(7), 0x7(0), 0x3(3), 0x3(0), 0x1(1), 0x1(0)
[Number in parentheses repeated to fill out number to comparator
size.]
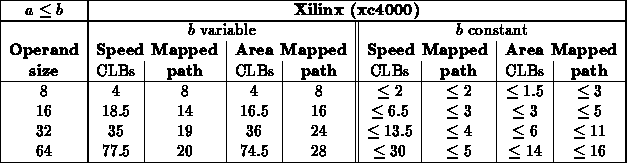
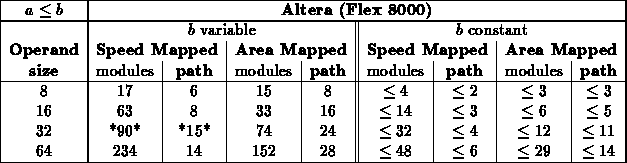
Range ( )
)
- For this test, a scattered sampling of values where used.
- 8 [0x80
 0x40], [0x64
0x40], [0x64 0x0A],
[0x17
0x0A],
[0x17 0x11], [0xC8
0x11], [0xC8 0x96],
[0xa7
0x96],
[0xa7 0x03], [0x78
0x03], [0x78 0x28],
[0x78
0x28],
[0x78 0x2A], [0x78
0x2A], [0x78 0x2B],
[0x79
0x2B],
[0x79 0x2B], [0xAA
0x2B], [0xAA 0x55],
[0x77
0x55],
[0x77 0x33], [0x77
0x33], [0x77 0x55],
[0x55
0x55],
[0x55 0x11], [0xEE
0x11], [0xEE 0x33],
[0xEE
0x33],
[0xEE 0x77]
0x77]
- 16,32,64 (digit in parenthesis repeated to fill up constant)
[0x8(0)0
 0x4(0)0], [0x8(0)0
0x4(0)0], [0x8(0)0 0x4(0)1],
[0x8(0)1
0x4(0)1],
[0x8(0)1 0x4(0)1], [0x9(0)9
0x4(0)1], [0x9(0)9 0x9(0)1],
[0x9(0)9
0x9(0)1],
[0x9(0)9 0x9(0)6], [0x9(0)9
0x9(0)6], [0x9(0)9 0x6(0)6],
[0x9(9)9
0x6(0)6],
[0x9(9)9 0x9(9)6], [0x9(9)9
0x9(9)6], [0x9(9)9 0x6(6)6],
[0xA(0)A
0x6(6)6],
[0xA(0)A 0x5(0)5], [0xA(0)A
0x5(0)5], [0xA(0)A 0x5(0)A],
[0xA(A)A
0x5(0)A],
[0xA(A)A 0x5(5)5], [0xC(0)1
0x5(5)5], [0xC(0)1 0x7(0)1],
[0xC(0)C
0x7(0)1],
[0xC(0)C 0x7(0)7], [0xC(C)C
0x7(0)7], [0xC(C)C 0x7(7)7],
[0xE(0)1
0x7(7)7],
[0xE(0)1 0x3(0)1], [0xE(0)E
0x3(0)1], [0xE(0)E 0x3(0)3],
[0xE(E)E
0x3(0)3],
[0xE(E)E 0x3(3)3], [0xE(E)E
0x3(3)3], [0xE(E)E 0x7(7)7],
[0xD(D)D
0x7(7)7],
[0xD(D)D 0xB(B)B]
0xB(B)B]
- For this test, the range logic was constructed in two ways: the
natural
 , and
, and
 . The best results
(according to speed or area optimization) is included here.
. The best results
(according to speed or area optimization) is included here.

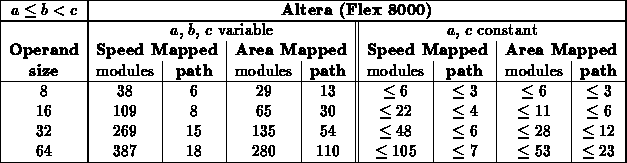
Generic Adders
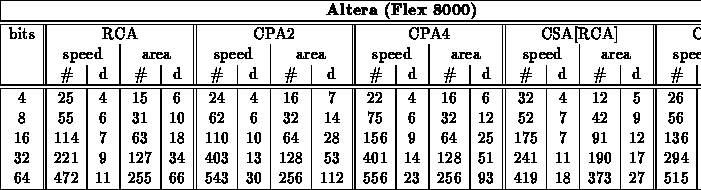
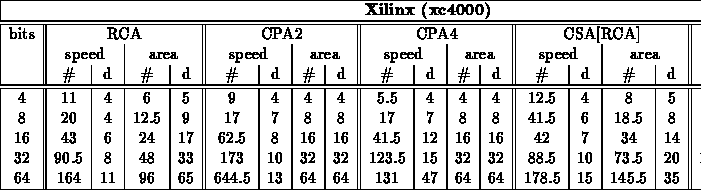
Specialized Adders
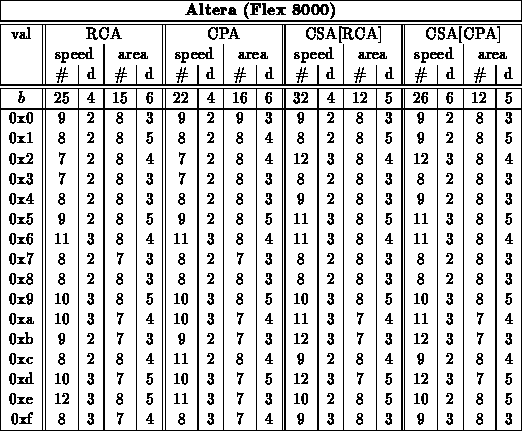

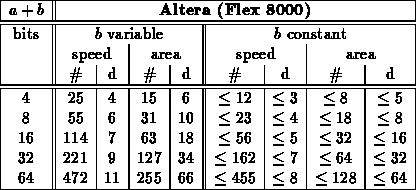
Note:
- Based on previous experiments, only used RCA adder here
- Table summarizes test of all cases for bits=4
- For larger values, projected strategic, worst-case patterns from
bits=4 experiment
- Patterns used
- size=8 - 00, EE, 77, 76, B7, 55, FF
- size=16,32,64 - 0*, E*, 7* (76)*, (B7)*, 5*, F*, (F77B)*, (76DB)*
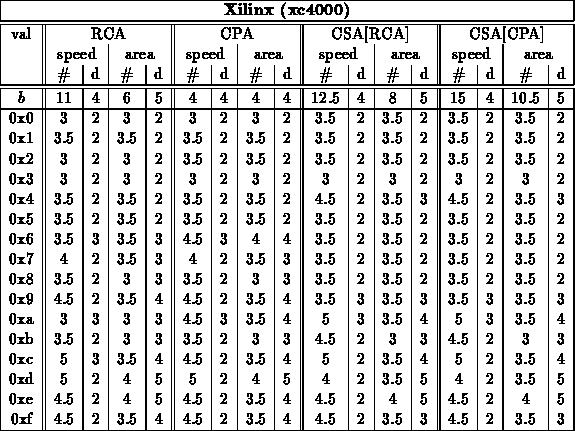

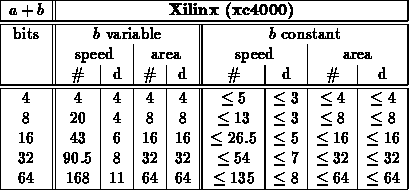
Note:
- Based on previous experiments, only used RCA adder here
- Table summarizes test of all cases for bits=4
- For larger values, projected strategic, worst-case patterns from
bits=4 experiment
- Patterns used
- size=8 - 00, EE, 77, 76, B7, 55, FF
- size=16,32,64 - 0*, E*, 7* (76)*, (B7)*, 5*, F*, (F77B)*, (76DB)*
- Final, specialized, speed mapped adder cases came from a combination
of running: fastest and mapped with target at fastest speed for group
crossed folding constant values into the unoptimized and optimized generic
designs

Note:
- Actually, for Xilinx, cpa case has better area mapping -- synthesizer
must be able to map to xilinx adder support in this case but not in
others...
- Here, we run both rca and cpa and take best
DES F Function
- For this test, one complete key schedule was used.


Here, we can be fairly certain we won't save anything other than the
initial, 48-bit XOR. Since the input can take on any value, the
output of the XOR can also take on any value, so there is no cascaded
savings reducing logic size in the S-boxes (of course, it was designed
that way).
Benefit and utility are marginal. In particular, for a given DES key, you
use the F box with 16 different keys,  . The specialization might be
beneficial if you fully unrolled the DES encoding. However, it's not clear
that is a good time/space tradeoff overall. Xilinx's 4010, for instance,
only has 400 CLBs. Unfortunately, the synthesis tools would not generate
an unrolled design in any reasonably short amount of time ( e.g. less
than 36 hours, at least).
. The specialization might be
beneficial if you fully unrolled the DES encoding. However, it's not clear
that is a good time/space tradeoff overall. Xilinx's 4010, for instance,
only has 400 CLBs. Unfortunately, the synthesis tools would not generate
an unrolled design in any reasonably short amount of time ( e.g. less
than 36 hours, at least).
METRO Foward Port FSM
MLINK node i/o FSM

- In dummy0 case no need for a separate dummy cycle counter (which is
needed in programmed dummy cycles case)
MLINK central FSM

I8251 (USART) Processor I/O FSM

I8251 (USART) Transmitter FSM

I8251 (USART) Receiver FSM

METROJR Router
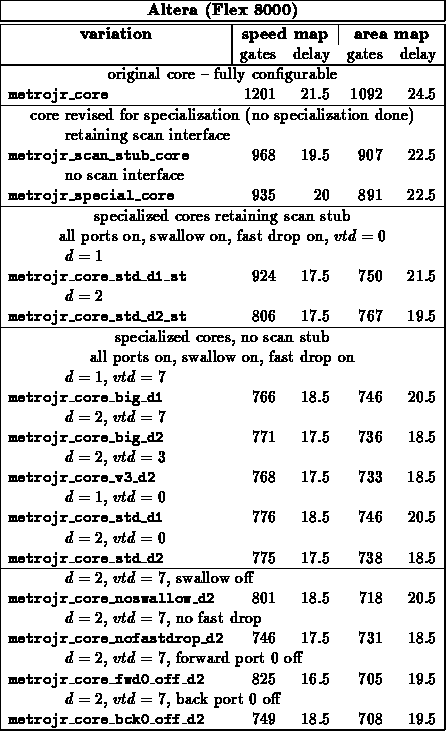

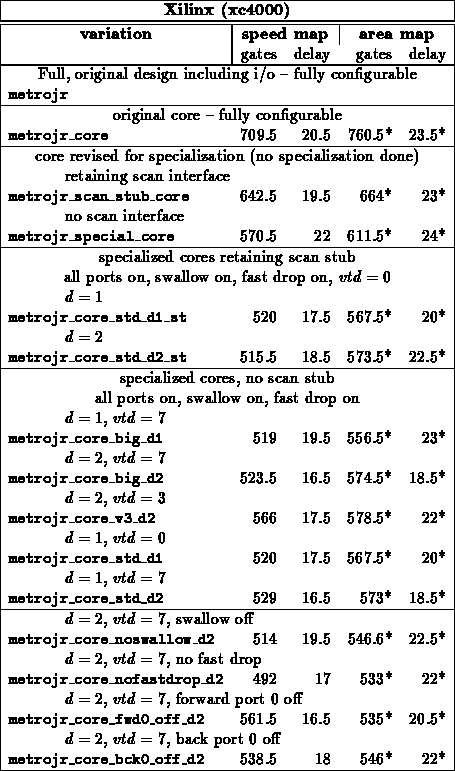
I8251 USART

by summarizing a collection of specialization
experiments. We follow the summary up by highlighting a few other
specializations which have been used in contemporary reconfigurable designs
in Section
. In Section
we discuss the
benefits of specialization, and in Section
we discuss when it is
advantageous to specialize.
summarizes specialization results for a number
of logic circuits. For each function, several sizes of operation are
given, as well as the worst-case size and speed across the specialized
values. In general, the specialized instances have a slightly shorter
critical path while requiring significantly less area.
are larger and slower than
typical Xilinx adders. The synthesis tools did not map to the specialized
carry logic available on the Xilinx array. Early Xilinx software only
exported this feature through its adder hard macro so the carry resource
can only be employed when custom adder blocks are inserted in the design
and not when the adder function is being inferred from logic. Using the
fast carry support, an
-bit adder can be implemented in
CLBs [Xil93].
summarizes several finite-state machine designs which can
be specialized around various configurations.
summarizes specializations for the core of
METROJR and the core of an I8251 USART. Both designs include all the core
logic up to, but not including, i/o pads. Both design include a mix of
FSMs, control logic, and datapaths.
. Nonetheless,
the specialized designs are generally faster than the speed mapped generic
design while being smaller than the area mapped generic design. Further,
routed delays are likely to display a greater savings for the smaller,
specialized design.



) is indepdendent of constant
value. The logic breaks down to:
known,
becomes either
or
. The presence or absence of the inversion on
is irrelevant for most FPGA technologies since the polarity inversion
can almost always be folded into the primitive logic cells at no additional
cost in logic.

















. The specialization might be
beneficial if you fully unrolled the DES encoding. However, it's not clear
that is a good time/space tradeoff overall. Xilinx's 4010, for instance,
only has 400 CLBs. Unfortunately, the synthesis tools would not generate
an unrolled design in any reasonably short amount of time ( e.g. less
than 36 hours, at least).









